by Jishnu Mehra
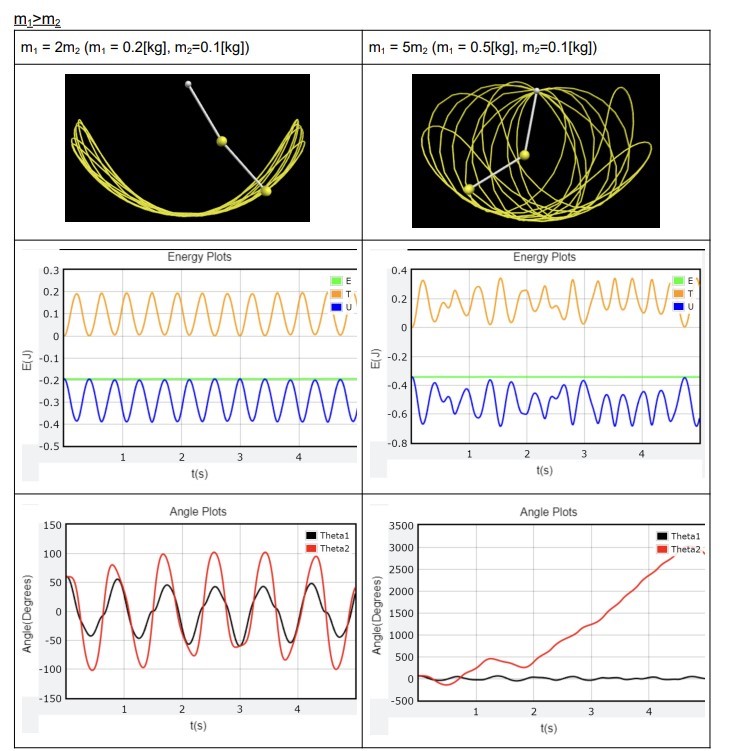
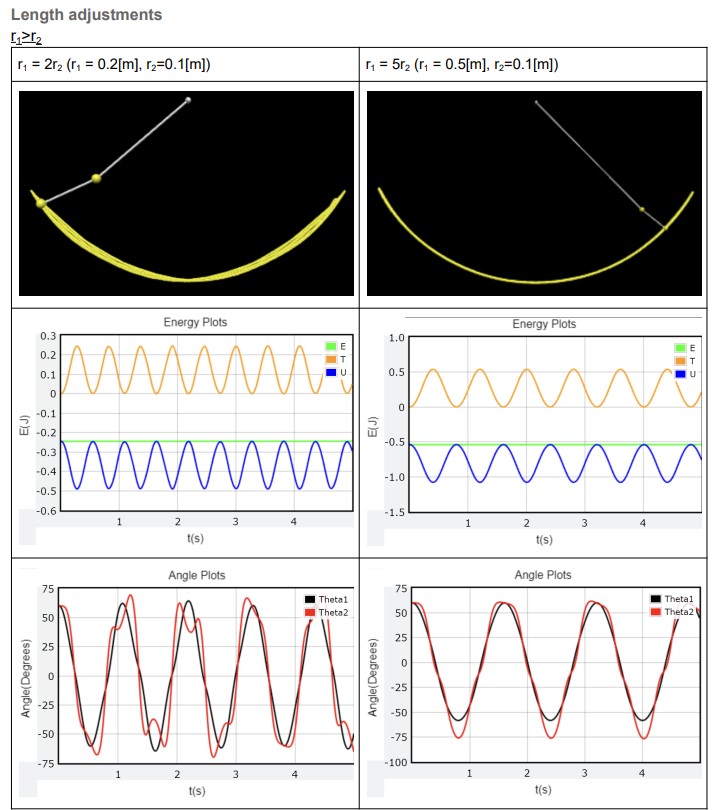
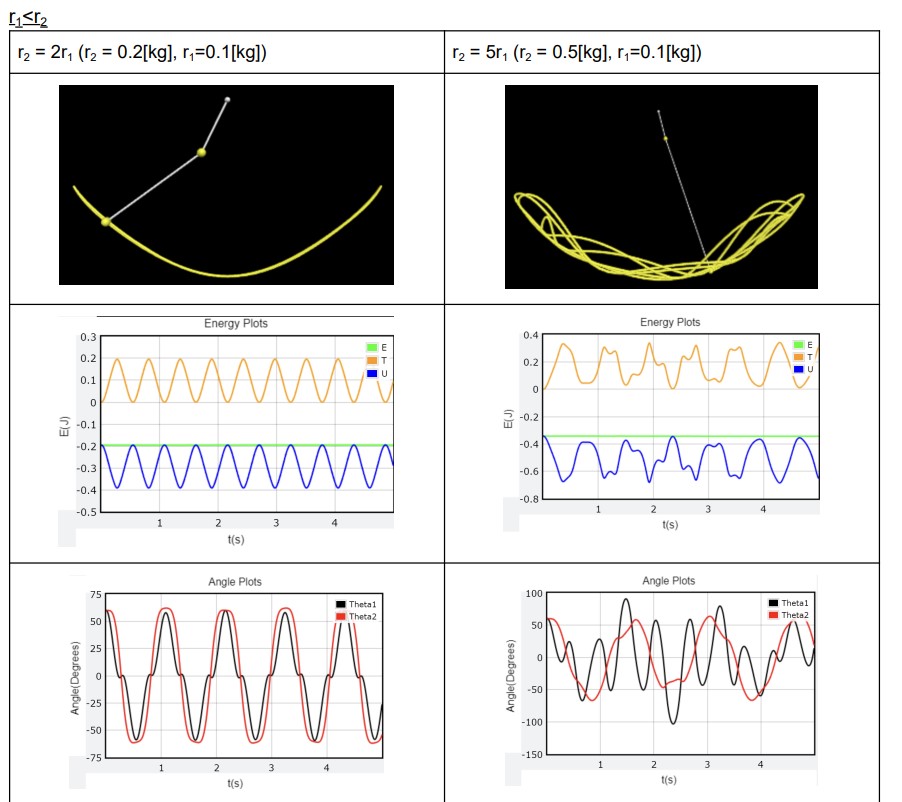
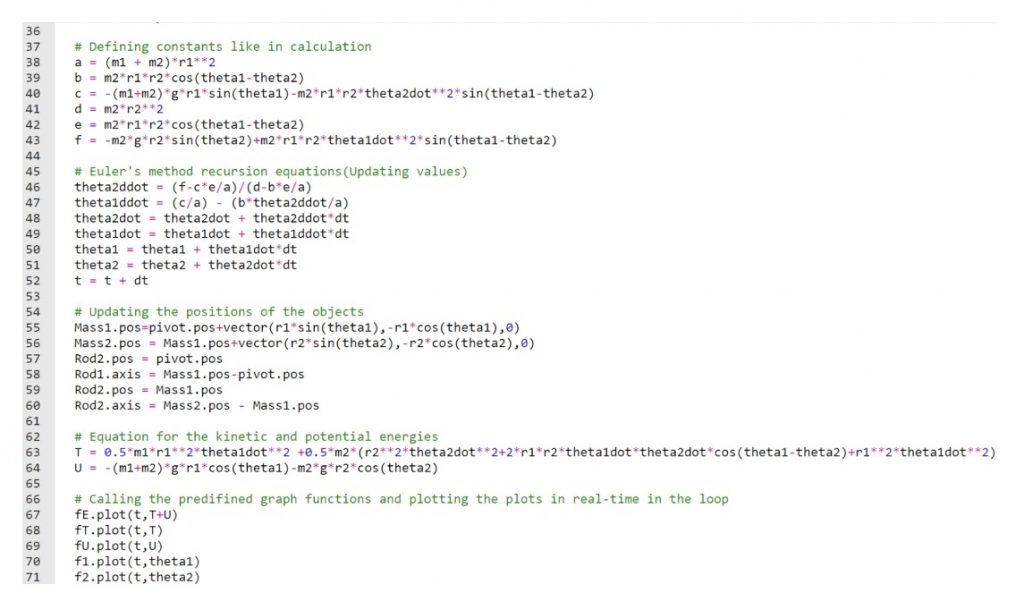
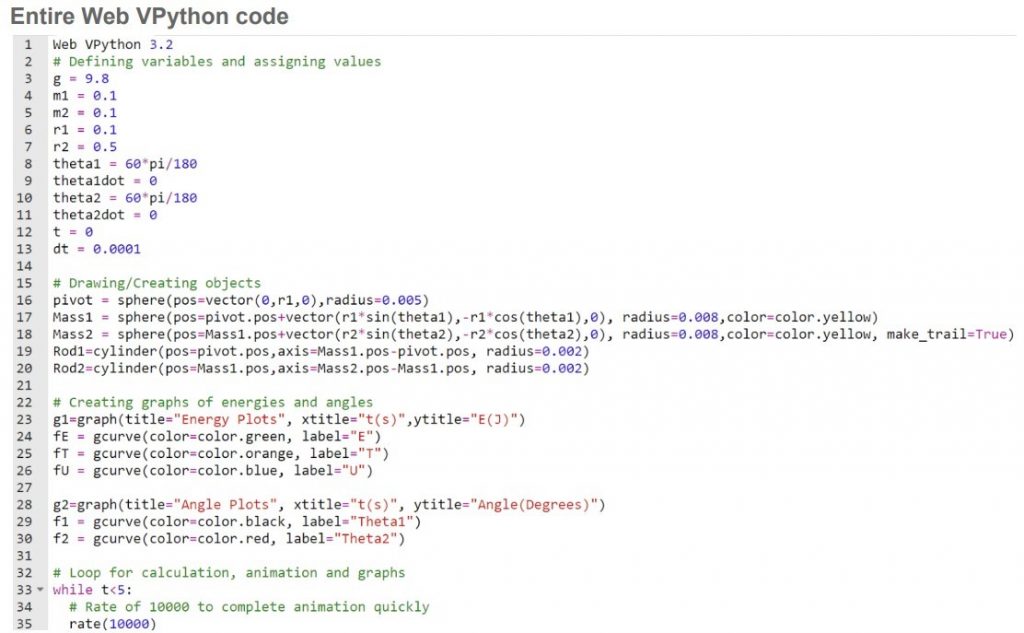
Project Description: The project endeavors to simulate the chaotic behavior of a double-layered pendulum using the Euler-Lagrangian second-order differential equation framework. It underscores the importance of preserving initial conditions to maintain the periodicity of pendulum motion. The learner demonstrated meticulousness in identifying pivotal parameters significantly influencing pendulum motion, namely mass, length, and angle. Given the dynamic nature of the system requiring testing against various initial conditions, the learner initially derived the theoretical second-order differential equation. Subsequently, the learner devised an algorithm based on this logic, implemented through Web V Python. The resultant simulator displayed the trajectory of motion, enabling the discernment of conditions leading to chaotic behavior over time versus those sustaining periodic motion. The project was self-initiated, showcasing the learner’s critical, creative, and analytical thinking. Ultimately, the project’s success is evident in the visual representation of pendulum motion generated via Web V Python, facilitating the identification of initial conditions conducive to chaos versus periodic phenomena. It was a part of Math HL Analysis and Approaches Internal Assessment.
Project Outcome: Visual representation of pendulum motion generated via Web V Python, facilitating the identification of initial conditions conducive to chaos versus periodic phenomena